Relativité générale et tenseur métrique

Le tenseur métrique est un élément central de la théorie de la relativité générale, sorte d’extension du théorème de Pythagore, il s’agit un objet mathématique qui permet de formaliser la notion de distance en espace courbe. Il est la quantité $g_{\mu \nu}$ qu’on cherche à déterminer dans l’équation d’Einstein

$$\begin{aligned} R_{\mu \nu} - \frac{1}{2} R g_{\mu \nu} + \Lambda g_{\mu \nu} = \frac{8 \pi G}{c^4} T_{\mu \nu} \end{aligned}$$

Et c’est à lui que nous allons nous intéresser aujourd’hui. Ce qui suit est en grande partie extrait du livre Mécaniques - des fragments d’espace-temps à paraître très prochainement.

Introduction

On ne peut appréhender la géométrie d’un espace sans s’accorder au préalable sur une façon d’y définir une distance. L’idée de distance est assez simple quand on se donne un système de coordonnées cartésien dans un espace euclidien mais les choses se compliquent pour des espaces plus exotiques tel celui de la relativité générale.

Nous allons introduire ici un objet mathématique particulier qui a pour nom le « tenseur métrique ». Quand par la suite nous parlerons de la métrique d’un espace, nous ferons indistinctement allusion à une fonction qui caractérise la distance dans cet espace et au tenseur métrique qui permet à lui seul de définir cette fonction et s’identifie donc avec.

La notion de tenseur et celle de géométrie courbe ne seront pas explicitées ici. Elles ne sont pas nécessaires à la compréhension de ce qui va suivre. Il suffira pour la première d’en représenter l’idée par une matrice, et on pourra pour ce qui est des géométries courbes se contenter d’en avoir une image intuitive.

Distance dans l’espace euclidien

En géométrie euclidienne, l’espace-temps est plat, et en coordonnées cartésiennes on peut facilement calculer la distance entre deux points grace au théorème de Pythagore. Soit $A$ et $B$ deux points d’un tel espace, aux coordonnées respectives $(x_A, y_A, z_A)$ et $(x_B, y_B, z_B)$, la distance noté ici $s$ entre $A$ et $B$ nous est donnée par

$$\begin{aligned} s = \sqrt{(x_B-x_A)^2 + (y_B-y_A)^2 + (z_B-z_A)^2} \end{aligned}$$

Si l’on retire la racine à droite, le carré de la distance $s$ devient la somme des carrés des distances entre les coordonnées des points dans chacune des dimensions.

On peut adopter une écriture plus concise si on écrit $A$ et $B$ sous la forme $(x_1, x_2, x_3)$ et $(y_1, y_2, y_3)$.
Les indices ne représentent alors plus ici le point, mais la dimension, et les lettres ne représentent alors plus les dimensions, mais les points. Nous aurions pu écrire $(A_1, A_2, A_3)$, mais on a préféré ici abandonner la référence explicite au nom du point d’origine pour nous conformer aux usages dans les notations.

Dès lors nous pouvons écrire l’équation précédente sous une forme réduite et indépendante du nombre de dimensions

$$\begin{aligned} s^2 = \sum_{i} (y_i - x_i)^2 \end{aligned}$$

La relativité générale, comme toute la physique, utilise l’ensemble des nombres réels pour représenter les phénomènes. Dès lors, entre deux points quelconques, il existe une infinité de points, aussi il nous est possible d’imaginer une distance qui soit aussi petite que l’on veut.

Si on considère à présent une telle distance infinitésimale $\textit{d}s$ entre deux points, de même que $\textit{d}x_i$ les distances infinitésimale entre les coordonnées de ces points, ou dit autrement, leur projection sur les axes correspondant aux dimensions $i$ de sorte que nous ayons $A(x_1, x_2, x_3)$ et $B(x_1 + \textit{d}x_1, x_2 + \textit{d}x_2, x_3 + \textit{d}x_3)$ on peut écrire

$$\begin{aligned} \textit{d}s^2 = \sum_{i} \textit{d}x_i^2 \end{aligned}$$

On remarquera, que les $\textit{d}s$ ne sont généralement pas égaux aux $\textit{d}x_i$ alors qu’il s’agit dans les deux cas de quantités infinitésimales aussi petites que l’on veut. Il faut comprendre ici que si conceptuellement ces quantités peuvent être aussi petites que l’on veut, ce qui nous intéresse se sont les relations qu’elles entretiennent.

Si le point $A$ à comme coordonnées (0, 0) et le point $B$ (1, 1), la distance de $A$ à $B$ sera de √2. On a défini le repère de manière à ce que $x_B$ et $y_B$ valent 1, mais c’est un choix arbitraire. On aurait pu les fixer à 0,1 ou 0,01 ou aussi petit que l’on veut.

Ce qui compte, ce ne sont pas les nombres fixés au départ, mais les distances que l’on peut mesurer ensuite qui en dépendent. Le résultat du calcul dépend des valeurs choisies, mais les distances relatives entre les points restent elles invariantes. Si la distance de $B$ à $C$ est 3 fois la distance de $A$ à $B$. Que l’on quadrille l’espace par pas de 1, de 0,1 ou 0,01 ou autre ne change rien à ce rapport.

$\textit{d}s$ doit être vu comme une quantité infinitésimale, ou aussi petite que l’on veut, ou suffisamment petite. Ce qui est vraiment important dans la géométrie différentielle ce sont les relations qui lient ces quantités, les distances, entre elles.

Pour un espace euclidien en représentation cartésienne, nous pouvons même remarquer que $\textit{d}s^2 = n\textit{d}x^2$, avec $n$ qui est la dimension de l’espace. Nous pourrions en rester là, mais nous voulons adopter une forme qui soit la plus générale possible afin que nous puissions la réutiliser pour des espaces non euclidiens.

Pour cela, nous allons introduire une fonction particulière $\delta(i,j)$ qui sera appelée par la suite le “delta de Kronecker”, et que nous définissons ainsi

$$\begin{aligned} \delta_{ij} = \delta_i^j = \delta^{ij} = \begin{cases} 1 & \text{si $i = j$} \\ 0 & \text{si $i \neq j$} \end{cases} \end{aligned}$$

Vous remarquerez la présence d’indices en haut et/ou en bas. Dorénavant, nous pourrons utiliser de tels indices indifféremment et écrire aussi bien $A(x_1, x_2, x_3)$ que $A(x^1, x^2, x^3)$. Pour le moment, le sens sera le même, mais vous verrez que l’intérêt apparaitra ensuite à l’usage. Enfin, vous pouvez voir le delta de Kronecker comme une matrice diagonale composée uniquement de 1 positifs. Ici en dimension 3, nous avons

$$\begin{aligned} [\delta_{ij}] = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{aligned}$$

A partir de la, nous pouvons écrire

$$\begin{aligned} ds^2 = \sum_{i=1}^n \sum_{j=1}^n \delta_{ij} \textit{d}x^i \textit{d}x^j \end{aligned}$$

Cette écriture est équivalente à la précédente. Elle est plus générale, mais elle peut sembler aussi un peu plus difficile à comprendre. Nous allons l’expliciter, mais avant cela, nous l’écrirons sous une forme plus réduite encore, nommée convention d’Einstein.

$$\begin{aligned} ds^2 = \delta_{ij} \textit{d}x^i \textit{d}x^j \end{aligned}$$

Nous avons retiré les opérateurs de sommation. Par convention, quand on rencontre des indices en haut et en bas répétés comme ici, on doit en effectuer la somme comme si le signe somme était présent. C’est une façon très répandue d’alléger les écritures. Nous allons maintenant expliciter le calcul

$$\begin{aligned} ds^2 = \sum_{i=1}^n \sum_{j=1}^n \delta_{ij} \textit{d}x^i \textit{d}x^j = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \textit{d}x^i \textit{d}x^j \end{aligned}$$ $$\begin{aligned} ds^2 &= \boldsymbol{\delta_{11}} \boldsymbol{\textit{d}x^1} \boldsymbol{\textit{d}x^1} + \delta_{12} \textit{d}x^1 \textit{d}x^2 + \delta_{13} \textit{d}x^1 \textit{d}x^3 \\ &+ \delta_{21} \textit{d}x^2 \textit{d}x^1 + \boldsymbol{\delta_{22}} \boldsymbol{\textit{d}x^2} \boldsymbol{\textit{d}x^2} + \delta_{23} \textit{d}x^2 \textit{d}x^3 \\ &+ \delta_{31} \textit{d}x^3 \textit{d}x^1 + \delta_{32} \textit{d}x^3 \textit{d}x^2 + \boldsymbol{\delta_{33}} \boldsymbol{\textit{d}x^3} \boldsymbol{\textit{d}x^3} \end{aligned}$$

Sont uniquement différent de zero les produits dont le delta de Kronecker est égal à 1 (en gras). Quand il est possible de confondre les indices en haut et la puissance carré, les $\textit{d}x^i$ sont mis entre parenthèses pour éviter toute confusion. Nous avons donc

$$\begin{aligned} ds^2 = (\textit{d}x^1)^2 + (\textit{d}x^2)^2 + (\textit{d}x^3)^2 = \sum_i (\textit{d}x^i)^2 = \sum_i \textit{d}x_i^2 \end{aligned}$$

Nous avons bien retrouvé ici l’équation $ds^2 = \sum_i \textit{d}x_i^2$, et c’est cette équation, sous la forme $ds^2 = \delta_{ij} \textit{d}x^i \textit{d}x^j$ qui est appelée la métrique. C’est le delta de Kronecker qui joue le role de tenseur métrique. Vous remarquerez que les $\textit{d}x^i$ n’ont plus vraiment d’importance.

Toute la logique de la métrique se retrouve dans le tenseur métrique, ici $\delta_{ij}$. C’est lui qui avec des coefficients judicieusement choisis va déterminer la manière de caractériser une distance dans l’espace, et c’est pour ça qu’on peut ainsi identifier la métrique au tenseur métrique, et que l’on pourra parler indistinctement de l’un comme de l’autre.

Distance dans l’espace de Minkowski

L’espace de Minkowski est celui de la relativité restreinte. C’est un espace-temps plat, c’est-à-dire sans courbure, mais qui différe très légérement de l’espace euclidien que nous venons de voir.

On parle en termes plus technique d’espace pseudo-euclidien, pour le différencier des espaces non euclidiens qui vont nous intéresser par la suite. N’étant pas euclidien, sa métrique différe très légérement de celle que nous venons de voir. En pratique, nous l’écrirons ainsi

$$\begin{aligned} ds^2 = \eta_{\mu \nu} \textit{d}x^\mu \textit{d}x^\nu \end{aligned}$$

Nous avons remplacé les indices $i$ et $j$ par $\mu$ et $\nu$. C’est équivalent, mais c’est ici seulement une question d’usage, l’emploi de lettres grecques signifie implicitement que nous travaillons maintenant en quatre dimensions. Le $\eta$ désigne ici le tenseur métrique de l’espace de Minkowski que l’on peut représenter par la matrice suivante

$$\begin{aligned} \eta_{\mu \nu} \equiv \begin{bmatrix} -1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \end{aligned}$$

Nous n’avons pas ici placé comme plus haut le $\eta$ entre crochets car il s’agit par définition d’une matrice. Dans le cas du symbole de Kronecker $\delta_{ij}$ il s’agit par définition d’une fonction de $i$ et de $j$ et nous nous intéressions à la matrice correspondante pour des $i$ et $j$ allant de 1 à 3.

Nous avons utilisé un triple égal à la place d’une égalité, car en toute exactitude il s’agit ici d’une équivalence logique ou d’une définition. Si nous réalisions explicitement le calcul, comme au dessus, nous obtiendrions

$$\begin{aligned} ds^2 = -(\textit{d}x^1)^2 + (\textit{d}x^2)^2 + (\textit{d}x^3)^2 + (\textit{d}x^4)^2 \end{aligned}$$

Et si on remplace enfin les $x^i$ par $t$, $x$, $y$, $z$, et que nous multiplions $\textit{d}t^2$ par $c^2$ (le temps $t$ s’exprime en seconde, et les longueurs $x$, $y$, $z$ en mètre. En multipliant $t$ par $c$, la vitesse de la lumière en mètre par seconde, nous pouvons traiter numériquement le temps comme une longueur), nous avons donc

$$\begin{aligned} ds^2 = -c^2 \textit{d}t^2 + \textit{d}x^2 + \textit{d}y^2 + \textit{d}z^2 \end{aligned}$$

Nous retrouvons ici l’intervalle caractéristique de la relativité restreinte, nous allons maintenant nous intéresser aux géométries riemanniennes.

Interlude

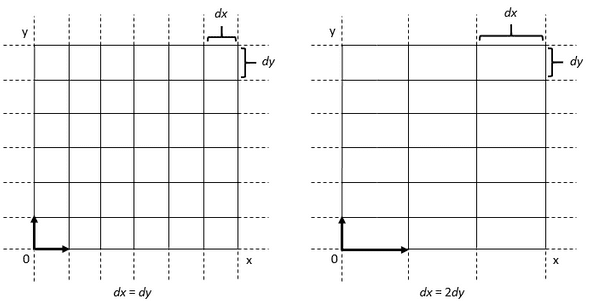
Jusqu’ici, nous avons seulement considéré des systèmes ou les coordonnées sont égales entre elles, une sorte de grille homogène qui recouvrirait tout l’espace. A présent, et sans changer encore de géométrie, nous allons rendre à peine plus complexe notre système de coordonnées en imaginant que $\textit{d}x = 2\textit{d}y$. Nous aurions alors quelques chose comme cela

En d’autres termes, en revenant à la notation indicielle, avec $\textit{d}x^1$ pour $\textit{d}x$ et $\textit{d}x^2$ pour $\textit{d}y$, nous avons $\textit{d}x^1 = 2\textit{d}x^2$. Nous voyons donc que notre système de coordonnées est défini de façon à ce que quel que soit la taille du plus petit intervalle $\textit{d}x^1$, l’intervalle $\textit{d}x^2$ sera toujours deux fois plus grand.

Physiquement on pourrait imaginer un tel espace comme un univers non homogène et dans lequel les directions ne se valent pas. Si je lance un objet vers le haut ($\textit{d}x^1$) et un autre vers la gauche ($\textit{d}x^2$), le second me paraîtra toujours filer deux fois plus vite que le premier.

On peut également imaginer qu’il s’agisse seulement d’un choix pratique de coordonnées pour une raison ou une autre. Charge au physicien de garder à l’esprit le lien entre l’espace réel et celui de sa représentation.

Cet exemple est ici trivial, et non représentatif d’une géométrie particulière (cela reste un espace plat), mais c’est une manière de s’imaginer, comment d’un point de vue einsteinien les phénomènes physiques et leur représentation géométrique peuvent être liés.

Distance dans les espaces riemanniens

Nous savons que la quantité $\textit{d}s$ peut varier en fonction des $\textit{d}x^i$, et nous supposerons maintenant que les $\textit{d}x^i$ eux même puissent aussi varier en fonction des points considérés. Aussi nous avions $A(x_1, x_2, x_3)$ et $B(x_1 + \textit{d}x_1, x_2 + \textit{d}x_2, x_3 + \textit{d}x_3)$, et nous allons maintenant avoir $A(x_1, x_2, x_3)$ et $B$($x_1 + f_1(x_1, x_2, x_3)$, $x_2 + f_2(x_1, x_2, x_3)$, $x_3 + f_3(x_1, x_2, x_3)$). Autrement dit, le $dx^i$ devient une quantité variable et fonction des coordonnées du point considéré.

De façon plus rigoureuse, les $x_i$ étaient des coordonnées cartésiennes, que nous noterons maintenant $y^i$, et nous introduisons à présent des coordonnées $x^i$ plus générales par la relation

$$\begin{aligned} x^i = x^i(y^1, y^2, y^3) \end{aligned}$$

Nous avons alors

$$\begin{aligned} \textit{d}x^i = \frac{\partial x^i}{\partial y^j} \textit{d}y^j \end{aligned}$$

---

Ce genre d’équation est plus simple qu’il n’y parait. Pour $\textit{d}x^1$ par exemple, si on l’écrit explicitement, nous avons dans le cas général

$$\begin{aligned} \textit{d}x^1 = \frac{\partial x^1}{\partial y^1} \textit{d}y^1 + \frac{\partial x^1}{\partial y^2} \textit{d}y^2 + \frac{\partial x^1}{\partial y^3} \textit{d}y^3 \end{aligned}$$

Dans les cas qui nous intéressent les variations partielles des $x^i$ seront indépendantes de celles des $y^j$ quand $i$ sera différent de $j$. Aussi, nous pourrions avoir

$$\begin{aligned} \textit{d}x^1 = \frac{\partial x^1}{\partial y^1} \textit{d}y^1 \end{aligned}$$

Equation que nous pourrions lire comme $\textit{d}x^1$ est égal à $\textit{d}y^1$ multiplié par de combien varie $\partial x^1$ quand $\partial y^1$ varie d’une unité. Ou la dérivé partielle de $x^1$ par rapport à $y^1$. Nous permettant de traduire un système de coordonnées dans un autre.

---

Tout ceci nous permet alors d’écrire la métrique de la façon suivante (en renommant les indices)

$$\begin{aligned} \textit{d}s^2 = \delta_{ek} \frac{\partial x^e}{\partial y^i} \textit{d}y^i \frac{\partial x^k}{\partial y^j} \textit{d}y^j = \delta_{ek} \frac{\partial x^e}{\partial y^i} \frac{\partial x^k}{\partial y^j} \textit{d}y^i \textit{d}y^j \end{aligned}$$

Enfin, pour alléger l’écriture, on introduit la notation

$$\begin{aligned} m_{ij} = \delta_{ek} \frac{\partial x^e}{\partial y^i} \frac{\partial x^k}{\partial y^j} \end{aligned}$$

Ce qui nous permet d’écrire le tenseur métrique sous la forme

$$\begin{aligned} \textit{d}s^2 = m_{ij} \textit{d}x^i \textit{d}x^j \end{aligned}$$

Nous allons à présent réaliser une petite application pratique en calculant une métrique. Supposons données les fonctions $x^i$ suivantes

$$\begin{aligned} &x^1 = sin \, y^1 \, cos \, y^2 \\ &x^2 = sin \, y^1 \, sin \, y^2 \\ &x^3 = cos \, y^1 \end{aligned}$$

Pour calculer la métrique $m_{ij}$, il nous suffit de repartir de sa définition, et de dériver les $x^i$ par rapport aux $y^j$

$$\begin{aligned} &m_{11} = \delta_{ek} \frac{\partial x^e}{\partial y^1} \frac{\partial x^k}{\partial y^1} \\[10pt] &m_{11} = \frac{\partial x^1}{\partial y^1} \frac{\partial x^1}{\partial y^1} + \frac{\partial x^2}{\partial y^1} \frac{\partial x^2}{\partial y^1} + \frac{\partial x^3}{\partial y^1} \frac{\partial x^3}{\partial y^1} \\[10pt] &m_{11} = (sin \, y^2 \, cos \, y^3)^2 + (sin \, y^2 \, sin \, y^3)^2 + (cos \, y^2)^2 \\[10pt] &m_{11} = 1 \end{aligned}$$

On calcule de la même manière les autres composantes du tenseur, et on obtient

$$\begin{aligned} \textit{d}s^2 = (\textit{d}x^1)^2 + (x^1)^2 (\textit{d}x^2)^2 + (x^1 \, sin \, x^2)^2 (\textit{d}x^3)^2 \end{aligned}$$

Soit, dans les notations usuelles

$$\begin{aligned} \textit{d}s^2 = \textit{d}r^2 + r^2\textit{d}\theta^2 + r^2 \, sin^2 \, \theta \textit{d}\varphi^2 \end{aligned}$$

Ce qui nous donne enfin pour ce $m_{ij}$

$$\begin{aligned} m_{ij} \equiv \begin{bmatrix} 1 & 0 & 0 \\ 0 & r^2 & 0 \\ 0 & 0 & r^2 sin^2\theta \end{bmatrix} \end{aligned}$$

Il s’agit ici seulement de la métrique de l’espace euclidien en coordonnées sphériques. Pour passer d’un espace riemannien à un espace pseudo-riemannien, ou lorentzien, il nous suffira de remplacer dans $m_{ij}$ le $\delta_{ek}$ par $\eta_{\epsilon \kappa}$, et on renommera $m_{ij}$ en $g_{\mu \nu}$. Ce qui nous donnera

$$\begin{aligned} g_{\mu \nu} =\eta_{\epsilon \kappa} \frac{\partial x^\epsilon}{\partial y^\mu} \frac{\partial x^\kappa}{\partial y^\nu} \end{aligned}$$

Et nous permettra d’écrire le tenseur métrique ainsi

$$\begin{aligned} ds^2 = g_{\mu \nu} \textit{d}x^\mu \textit{d}x^\nu \end{aligned}$$

Ce qu’il nous faut enfin comprendre ici, c’est à quel point, le $g_{\mu \nu}$, le tenseur métrique, est central dans la théorie d’Einstein. C’est la métrique qu’on doit chercher et qui déterminera le tenseur de courbure, la forme de l’espace-temps, et donc la trajectoire de ses géodésiques, ses “lignes droites”.

Tenseur métrique et équation d’Einstein

Résoudre l’équation d’Einstein revient en pratique à trouver ce fameux $g_{\mu \nu}$. Le problème, c’est que cette équation n’est pas linéaire. On se donne en général une distribution particulière de matière, et en faisant preuve de dextérité, en suant un peu, on peut quelquefois trouver une solution exacte de cette équation.

Les exemples les plus connus étant la métrique de Schwarzschild qui décrit la courbure de l’espace-temps autour d’une masse sphérique, sans rotation, ni charge, la métrique de Kerr, lorsque la masse est en rotation, et celle de Kerr-Newman lorsque cette dernière possède en plus une charge électrique.

En plus de celles-ci, on a également la métrique de Friedmann-Lemaître-Robertson-Walker, ou FLRW, qui permet de décrire la courbure moyenne de l’univers à grande échelle et qui est à la base de toute la cosmologie contemporaine.

A titre d’exemples, voici celle de Schwarzschild

$$\begin{aligned} \textit{d}s^2 = - \boldsymbol{\left(1 - \frac{r_s}{r}\right)} c^2 \textit{d}t^2 + \boldsymbol{\left(1 - \frac{r_s}{r}\right)^{-1}} \textit{d}r^2 - r^2 (\textit{d}\theta^2 + sin^2 \theta \textit{d}\phi^2) \end{aligned}$$

On remarquera a quel point la métrique de Schwarzschild est similaire à celle de Minkowski exprimé en coordonnées sphériques.

$$\begin{aligned} \textit{d}s^2 =  - c^2 \textit{d}t^2 + \textit{d}r^2 - r^2 (\textit{d}\theta^2 + sin^2 \theta \textit{d}\phi^2) \end{aligned}$$

Arrivé là, nous avons une idée assez précise de ce qu’est le tenseur métrique. Nous avons ainsi remplacé le bon vieux théorème de Pythagore par une généralisation applicable à toute sorte d’espaces courbes.

Conclusion

On notera enfin pour conclure, que la terminologie de tenseur métrique constitue une économie de langage. Le tenseur métrique $g_{\mu \nu}$ est à proprement parlé une fonction des coordonnées qui désigne un champ de tenseurs. Le tenseur réel en un point se ramenant à une collection de nombres correspondant aux coefficients de la métrique.

Dans le chapitre consacré à la relativité générale du livre Mécaniques - des fragments d’espace-temps nous développons un peu plus ces idées, nous intéressant au principe d’équivalence, aux notions de courbure, de géodésiques et aux autres tenseurs de la théorie.

---

Recevoir régulièrement des articles comme celui-ci dans vos emails et toutes les infos du livre Mécaniques - des fragments d’espace-temps ? Abonnez vous à notre newsletter :